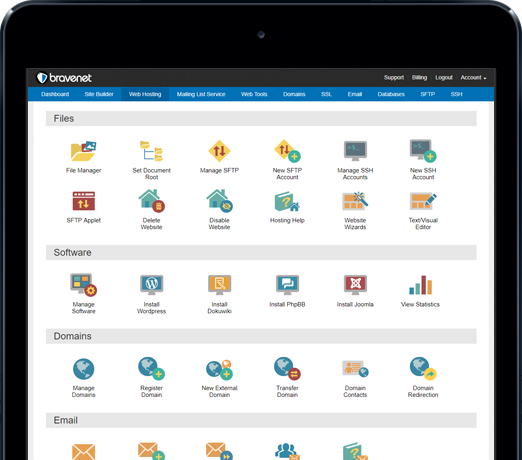
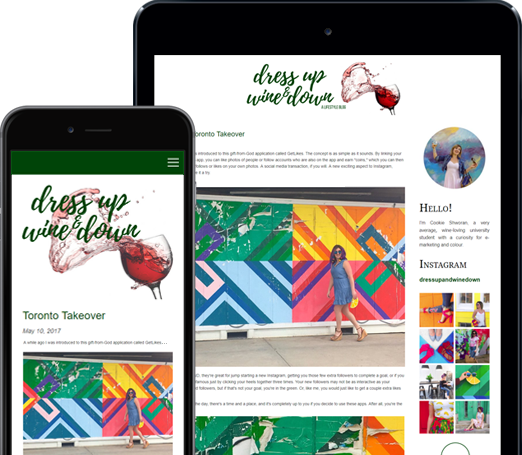
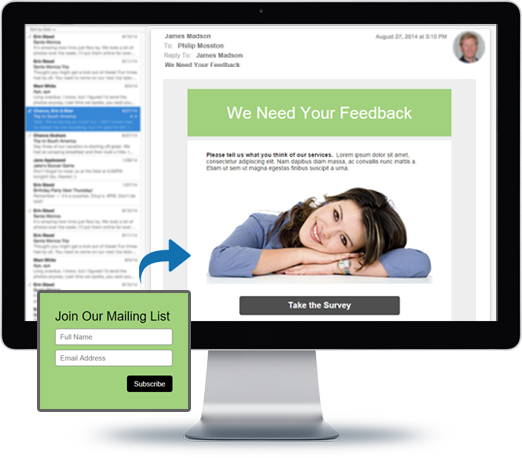
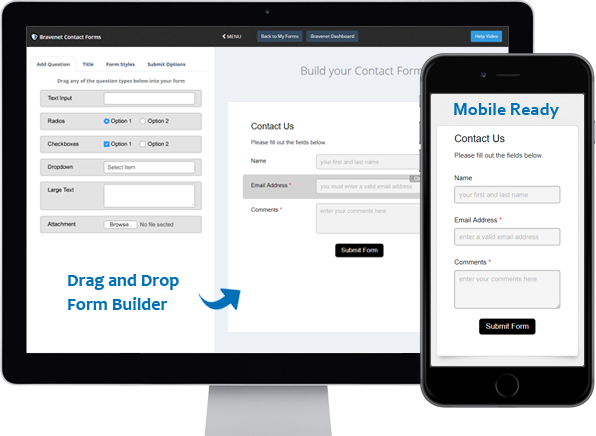
You can do so much at Bravenet
question_answer
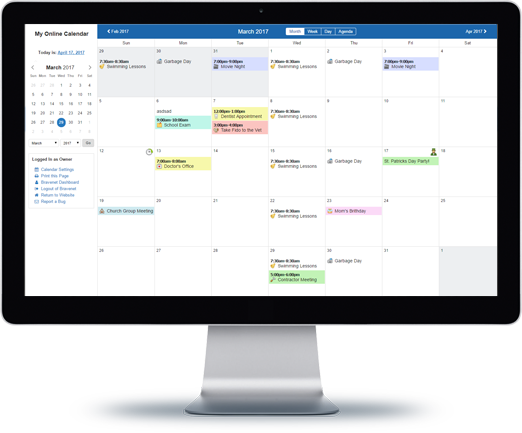
Message Boards
Forums allow you to easily
host online discussions
and build a community.
assignment_turned_in
Contact Forms
Use the easy Form Builder,
collect information and
even attachments.
import_contacts
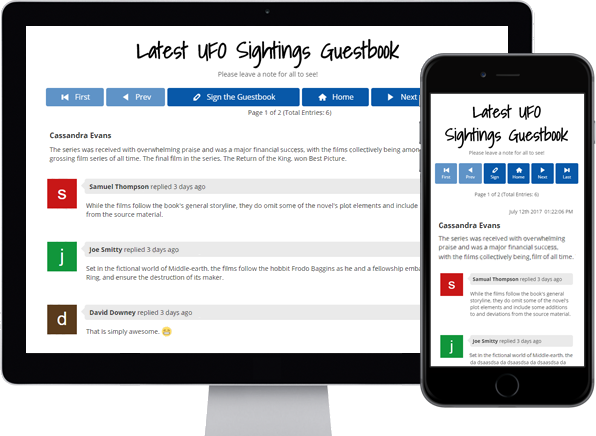
Guestbooks
Engage with your website
visitors by letting them post
in your Online Guestbook.
shopping_cart
BraveShop Stores
Sell your products online,
embed store on your site,
Start earning today!
public
Counters & Web Stats
Watch your website traffic
with live site statistics
and historical graphs.
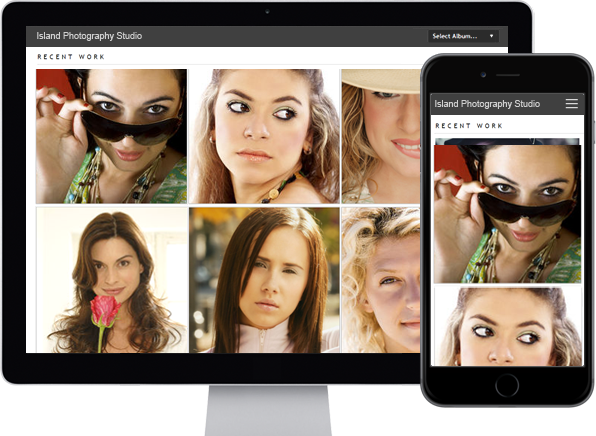
photo_library
Photo Albums
Store and share your photos
online, private or public,
Enable public uploads!
markunread_mailbox
Email Hosting
Feature-rich, reliable and
secure, with anti-spam and an
awesome email account manager.
camera_alt
Free Stock Photos
Bravenet Members enjoy
150,000 free stock photos
for use in sites & services.